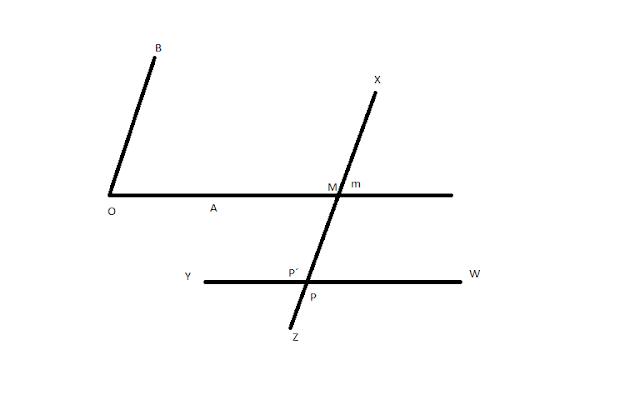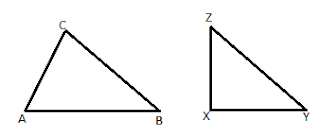TEOREMA XXX
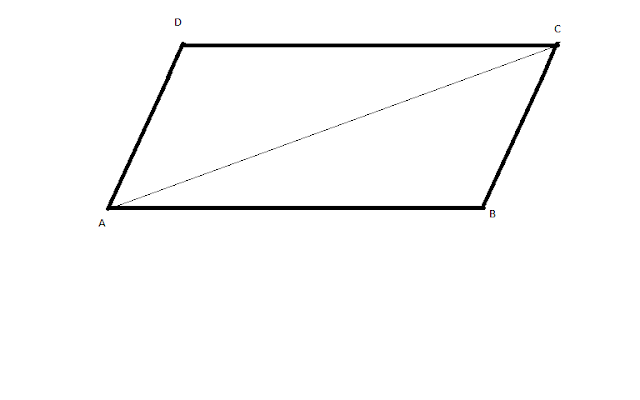
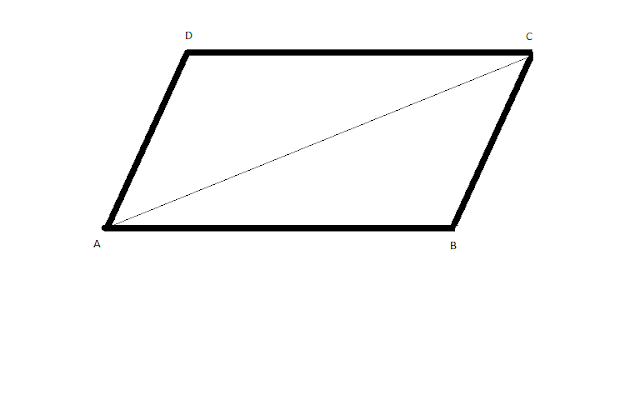
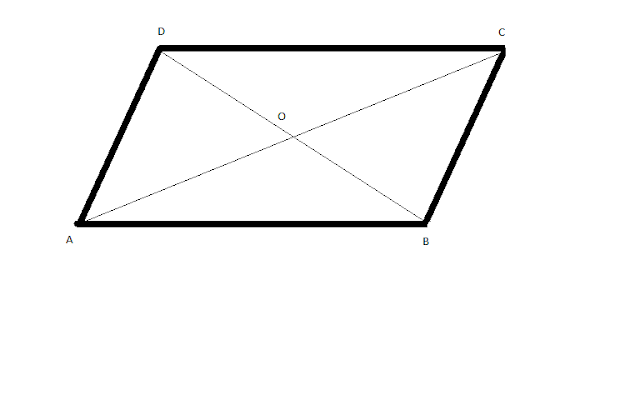
SI DOS LADOS ADYACENTES DE UN PARALELOGRAMO Y EL ANGULO COMPRENDIDO SON RESPECTIVAMENTE IGUALES A LOS DOS LADOS DEL OTRO LOS DOS PARALELOS SON IGUALES
AB=A’B’
AD=A’D’
<A=<A’
A’ caiga en A
A’B’ tomara la dirección de AB
A’D’ tomara la dirección de AD
D’ caera en D
B’ caera en B
<A=<A’ Pr definicon de angulos opuestos iguales
D’C’= DC TEOREMA 17
BC=B’C’
TEOREMA 31
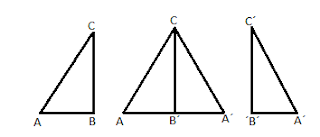
SI LOS SEGMERNTOS DETERMINADOS EN UNA TRANSVERSAL POR TRES O MAS PARALELAS SON IGUALES TAMBIEN LO SON IGUALES LOS DETERMINADOS EN CUALQUIERA OTRA TRASVERSAL POR LAS MISMAS PARALELAS
Demostrar que: AC=CE=EG
Ttrazamos AP,CQ,ER paralelas a BH
El <ADC,CQE,ERG, son respectivamente = BDC;DFE;FHG POR TEOREMA 18
<BDC=DFE=FHG POR TEOREMA 18
<CAB=<CQE=<ERG son igules por axioma 7
AP,CQ,ER son paralelas COROLALIO 2
<AP=ECQ=GER POR TEOREMA 8
AP=CQ=ER POR AXIOMA 7
Triángulos CPA=EQC=GRE POR TEOREMA 3
AC=CE=EG L.Q.Q.D
TEOREMA 32
LA SUMA DE LOS ANGULOS INTERNOS DE UN POLIGONO CUALQUIERA ES IGUAL A DOS RECTOS MULTIPLICADO POR EL ECCESO DE NUMERO DE LADOS SOBRE DOS
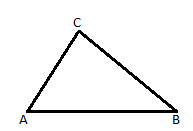
Sea el polígono ABCDEF
DEMOSTRAR <A+B+C+D+E+F= 180(n-2)
Desde el vértice F trazamos las diagonales y formamos (n-20 ) triangulo por que a cada lado le corresponde un triangulo menos a los de AF Y FE
Como la suma de los angulos interiores de un triangulo es= 180(2rectos) los (n-2) triángulos tendrán (n-2) rectos=180(n-2)
TEOREMA XXXIII
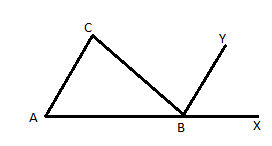
LA SUMA DE LOS ANGULOS EXTERNOS DE UN POLIGONO FORMADOS POR LA PROLONGACION SUCESIVA DE SUS LADOS ES IGUAL A 4 RECTOS
Sea el polígono ABCDEF en el que los angulos ecternos son a’b’c’d’e’f’
DEMOSTRAR QUE; a’b’c’d’e’f’= 4 rectos
<a=<a’= 180 por angulo de lados colineales
como el polígono tiene n pares de estos engulos la suma de todos los angulos internos es igual a n(2 restos)
como la suma de los angulos internos es (n-2)(rectos) tenemos que los angulos ecternos son igual a :
2nrectos-2nrectos=4rectos
4rectos L.Q.Q.D
TEOREMA 34
LA PERPENDICULAR BISECTRIZ DE UN SEGMENTO ES EL LUGAR GEOMETRICO DE TODOS LOS PUNTOS EQUIDISTANTES DE LOS EXTREMOS DEL SEGMENTO
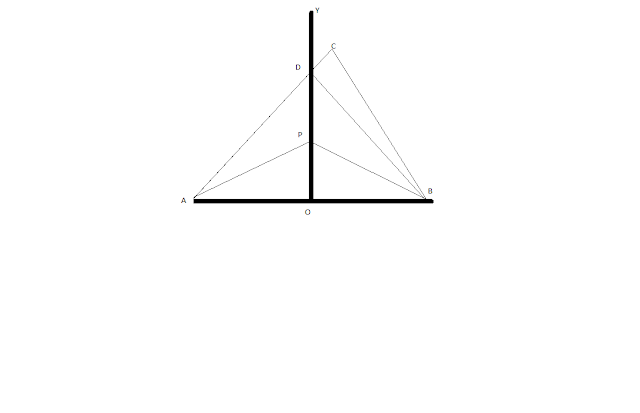
Sea OX la perpendicular bisectriz que bisecta del segemnto AB
Demostrar que: AP=BP Y AQ>QB
<AOP=<BOP perpendicular
AO=OB
PO=PO
Triángulos AOP=BOP TEOREMA 2
AP=BP partes homologas
BR+QR>BQ colorario3
BR=AR teorema anterior
AR+QR>BQ
AR+QR=BQ
AQ>BQ L.Q.Q.D
TEOREMA I
EN UN MISMO CIRCULO O EN CIRCULOS IGUALES ANGULOS CENTRALES IGUALES INTERCEPTAN ARCOS IGUALES Y EL MAYOR DE DOS ANGULOS DESIGUALES ITECEOTAN MAYOR ARCO
DEMOSTRAR
Arc AB=ARC A’B’
Arc AC>ARC A’B’
TRASLADAMOS EL CIRCULOo’ sobre el circulo o de tal suerte que sus centros coincidan o y o’
En consecuencia
A coincide A’
OB’ tomara la dirección que OB
B’ Coincide B
ARC AB= ARC A’B’
SI<COA><AOB, C caera fuera del arco AB
POR TANTO
Arc AC>arc AB
TEORENA 2
EN UN MISMO CIRCULO O EN CIRCULOS IGUALES ARCOS IGUALES SUBYIENDEN ANGULOS IGUALES Y EL MAYOR DE LOS ARCOS DESIGUALES SUBTIENDEN MAYOR ANGULO CENTRAR
Sean los círculos iguales O Y O’
DEMOSTRAR <AOB=<A’O’B’
Trasladamos el circulo o sobre el o’ de tal suerte que A coincida con A’
Como los radios son iguales O’
B’ coincide con B por hipótesis
<AOB=<A’O’C’ por superposición
<AOB><A’O’B’ POR AXIOMA 8
TEOREMA 3
EN UN MISMO CIRCULO O EN CIRCULOS IGUALES ARCOS IGUALES SON SUBTENDIDOS POR CUERDAS IGUALES Y EL MAYOR DE LOS ARCOS DESIGUALES ES SUBTENDIDO POR MAYOR CUERDA
DEMOSTRAR
CUERDA AB=CUERDA A’B’
OA=O’A’ radios iguales
OB=O’B’
Angulos AOB=A’O’B’ arcos igules
LOS DOS TRIANGULOS SON IGUALES POR TEOREMA 2
AB=A’B’
CUERDA AC>CUERDA AB L.Q.D.
TEOREMA 4
EN UN MISMO CIRCULO O EN CIRCULOS IGUALES CUERDAS IGUALES SUBTIENDEN ARCOS IGUALES EL MAYOR ARCO
DEMOSTRAR arco AB=A’B’
Trace
OA=O’A’
OB=O’B’
Cuerda AB=CUERDA A’B’
Los dos triángulos son iguales
<AOB=<A’O’B’
AB=A’B’
CUERDA AF =A’B’
TEOREMA 5
LA PERPENDICULAR TRAZADA POR EL CENTRO POR EL CENTRO DE UN CIRCULO O EN CUERDA BISECTA LA CUERDA Y LOS ARCOS SUBTENDIDOS
DEMOSTRACION
Tracese los radios OA=OB
Puesto que OM=OM
OA,OB
ASI MISMO ANGULO AOP= ANGULO BOP
ARC AQ= ARC BQ= ARCO AP