GEOMETRIA Y TRIGONOMETRIA: IdEnTiDaDeS tRiGOnOmEtRiCaS

domingo, 30 de octubre de 2011

IdEnTiDaDeS tRiGOnOmEtRiCaS

CONCEPTO

Es una igualdad entre expresiones que contienen funciones trigonometricas y es valida para todas las funciones del angulo en los que esta definida las funciones

Identidades trígonométricas fundamentales

Relación seno coseno

cos² α + sen² α = 1

Relación secante tangente

sec² α = 1 + tg² α

Relación cosecante cotangente

cosec² α = 1 + cotg² α

Funciones trigonométricas en función de las otras cinco.
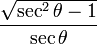sen	$\operatorname{sen} \theta\$	$\sqrt{1 - \cos^2\theta}$	$\frac{\tan\theta}{\sqrt{1 + \tan^2\theta}}$	$\frac{1}{\sqrt{1+\cot^2\theta}}$	$\frac{\sqrt{\sec^2 \theta - 1}}{\sec \theta}$	$\frac{1}{\csc \theta}$
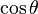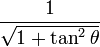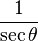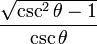cos	$\sqrt{1 - \operatorname{sen}^2\theta}$	$\cos \theta\$	$\frac{1}{\sqrt{1 + \tan^2 \theta}}$	$\frac{\cot \theta}{\sqrt{1 + \cot^2 \theta}}$	$\frac{1}{\sec \theta}$	$\frac{\sqrt{\csc^2\theta - 1}}{\csc \theta}$
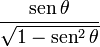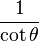tan	$\frac{\operatorname{sen}\theta}{\sqrt{1 - \operatorname{sen}^2\theta}}$	$\frac{\sqrt{1 - \cos^2\theta}}{\cos \theta}$	$\tan \theta\$	$\frac{1}{\cot \theta}$	$\sqrt{\sec^2\theta - 1}$	$\frac{1}{\sqrt{\csc^2\theta - 1}}$
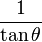cot	${\sqrt{1 - \operatorname{sen}^2\theta} \over \operatorname{sen} \theta}$	${\cos \theta \over \sqrt{1 - \cos^2\theta}}$	${1 \over \tan\theta}$	$\cot\theta\$	${1 \over \sqrt{\sec^2\theta - 1}}$	$\sqrt{\csc^2\theta - 1}$
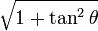sec	${1 \over \sqrt{1 - \operatorname{sen}^2\theta}}$	${1 \over \cos \theta}$	$\sqrt{1 + \tan^2\theta}$	${\sqrt{1 + \cot^2\theta} \over \cot \theta}$	$\sec\theta\$	${\csc\theta \over \sqrt{\csc^2\theta - 1}}$
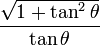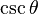csc	${1 \over \operatorname{sen} \theta}$	${1 \over \sqrt{1 - \cos^2 \theta}}$	${\sqrt{1 + \tan^2\theta} \over \tan \theta}$	$\sqrt{1 + \cot^2 \theta}$	${\sec \theta \over \sqrt{\sec^2\theta - 1}}$	$\csc \theta\$

.

No hay comentarios:

Publicar un comentario

Suscribirse a: Enviar comentarios (Atom)